start
\def \hvec#1{\hat{\vec{ #1}}} $\def \hvec#1{\hat{\vec{ #1}}}$
\def \part{\partial} $\def \part{\partial}$
\def \ket#1{\left|#1 \right >}$\def \bra#1{\left<#1 \right |}$
\def \bra#1{\left<#1 \right |}$\def \ket#1{\left|#1 \right >} $
\def \Braket#1{\left< #1 \right>} $\def \Braket#1{\left< #1 \right>}$
\def \Tr{\mathrm{Tr}} $\def \Tr{\mathrm{Tr}}$
\def \braket#1{\left< #1 | #1 \right>} $\def \braket#1{\left< #1 | #1 \right>}$
\def \qcc#1#2{[\hat{ #1 },\hat{ #2 }]}$\def \qcc#1#2{[\hat{ #1 },\hat{ #2 }]}$
\def \dd{\mathrm{d}} $\def \dd{\mathrm{d}}$
\def \Ket{\ket}$\def \Ket{\ket}$
\def \ppv#1{\frac{\part}{\part \vec #1}}$\def \ppv#1{\frac{\part}{\part \vec #1}} $
\def \set#1{\left\{ #1 \right\} } $\def \set#1{\left{ #1 \right} }$
\def \norm#1{\left| #1 \right|} $\def \norm#1{\left| #1 \right|}$
\def \tr{\Tr} $\def \tr{\Tr}$
oiint 暂时不知道怎么解决
end\
可以试着看看 note on QCQI.pdf 这个pdf
早就已经停止更新了,其实从七月暑校开始就摆了,感觉大概了解了一下量子算法就跑路了。
总体而言觉得还是挺好玩的,但没有特别喜欢,量子信息觉得略微有些——不是很喜欢。
三天速成简量)
这份笔记没有任何参考价值
《Nielsen, Chuang - Quantum Computation and Quantum Information - 10th》
不会真有东西吧,就我这四级都不会的废物)
https://dii.nju.edu.cn/a6/7b/c11317a566907/page.htm —— 怎么和暑校完全冲突啊
一部分是Nielsen的书,一部分是上面那个南京大学的项目(瞎摸鱼听一听)。
部分答案 : Solutions: Quantum Computation and Quantum Information by Nielsen and Chuang | Pseudo- (serab.net)
阿巴阿巴(好像可以用来预习高代应付回头考)(拓扑拾遗)
(先是一些看上去无关的w
引论部分
…好牛逼啊,我什么都不会嘿嘿…
狄拉克符号对反线性算符应该注明往哪个方向作用
linear algebra
$A$ 伴随变换 $\dagger$ 指的是 $(Au,v)=(u,A^\dagger v)$ 的那个东西,$(u,v)$ 在空间定义的一个半线性的函数,对于右边是完全线性的,左边的线性要共轭一下。
这个空间的名字叫什么呢?这已经是酉空间了,希尔伯特空间好像还要求柯西列收敛到柯西列,对那个半线性函数还有别的要求。
$(au,v)=a^*(u,v)\ \ \ \ (u,av)=a(u,v)$
一个众所周知的结论是 Cauchy-Schwarz inequality
一种证明是构造二次函数,取 $\lambda = (u,v)||v||^{-2}$
2.13
通过这个结论可以,投影变换 $P$ 的伴随是它自己
Suppose W is a k-dimensional vector subspace of the d-dimensional vector space V. Using the Gram-Schmidt procedure it is possible to construct an orthonormal basis $\ket 1,\dots ,\ket d$ for V such that $\ket 1,\dots,\ket d$ is an orthonormal basis for W. By definition
is the projector onto the subspace W.
同样可以定义 $Q\equiv I-P$ ,称为 $P$ 的正交补 orthogonal complement。it’s easy(????) to see that $Q$ is a projector onto the vector space spanned by $\ket {k+1},\dots,\ket d$ , which we also refer to as the orthogonal complement of $P$ , and may denote by $Q$
2.16 show that any projector $P$ satisfies the equation $P^2 = P$
Hermitian,normal,unitary
然后小伙子,你可以回忆一下有哪些神奇的变换
Hermitian or self-adjoint if $A^\dagger = A$
这个的特征值都是实数
normal if $AA^\dagger=A^\dagger A$ 容易发现 Hermitian 也是 normal 的
unitary if $U^\dagger U=I$. 酉矩阵是特殊的正规矩阵
2.17 Show that a normal matrix is Hermitian if and only if it has real eigenvalues.
A normal matrix A is diagonalized by an unitary matrix U such that
where $D$ is a diagonal matrix
Hermitian conjugate of A is
and $A=A^\dagger \iff D=D^\dagger \iff$ all eigenvalues are real
一个矩阵可酉对角化的充分必要条件是它是正规矩阵,但可对角化的矩阵不一定可以酉对角化
酉变换酉矩阵保持变换情况下内积的长度不变,也就把一组正交基变成一组正交基。
如果 $\ket {u_i},\ket {w_i}$ 是一组单位正交基,那么容易发现 $U\equiv \sum_i\ket {w_i}\bra {v_i}$ 是酉变换。
2.18 Show that all eigenvalues of a unitary matrix have modulus 1, that is, can be written in the form $e^{i\theta}$ for some real $\theta$.
2.19 Show that Pauli matrices are Hermitian and unitary
positive operators if $(v,Av)$ is real and $(v,Av)\ge 0$ for any $v\not=0$.
positive definite operators if $(v,Av) > 0$ for any $v \not=0$.
正定矩阵一定是自伴的
The spectral decomposition
谱分解定理(Spectral decomposition) Any normal operator $M$ on a vector space $V$ is diagonal with respect to some orthonormal basis for $V$ . Conversely, any diagonalizable operator is normal.
就是说正规矩阵一定可以对角化,可对角化的矩阵一定正规。怎么感觉lww之前提到过什么的样子。可交换就可以同时对角化?忘记了。诶,所以可以用那个方法搞吗——不知道
取特征值 $\lambda$ 和它的特征子空间上的投影变换 $P$,正交补 $Q$,这里有 $P^\dagger=P,P^2=P$
$M = (P+Q) M (P+Q)$ ,可以证明 $QMP=0,PMQ=(QM^\dagger P)^\dagger=0$
其中 $MM^\dagger \ket v=M^\dagger M\ket v=\lambda M^\dagger \ket v$ ,说明它的 $M^\dagger P$ 在 $Q$ 的零空间。
从而 $M=\lambda P+QMQ$,而 $QM=QM(P+Q)=QMQ$ 类似推出来 $QMQ$ 是正规的
归纳法得证
投影变换在一个子空间里面的话,那个矩阵还是对角的,这就很棒。
tensor products
张量积,外积,其中运算的定义都是很自然的
任何一个 $V\otimes W\to V’\otimes W’$ 的线性算子 $C$ 都可以写成 $A:V\to V’,B:W\to W’$ 的积的线性组合,$C=\sum_ic_iA_i\otimes B_i$
感觉是不是类似于矩阵展开的感觉
对于 $A,B$ 如上定义,有
用矩阵具体写的话,可以用 Kronecker product,就是分块然后展开。
2.28 $(A\otimes B)^=(A^\otimes B^*),(A\otimes B)^T=(A^T\otimes B^T),(A\otimes B)^\dagger=(A^\dagger\otimes B^\dagger)$
用Kronecker product展开即可
两个unitary算子,Hermitian算子,positive算子,projector算子的张量积依然保持性质。
Operator functions
定义相应的函数,所有特征值进行变换,即 $A=\sum_aa\ket a\bra a,f(A)=\sum_af(a)\ket a\bra a$
2.35 (Exponential of the Pauli matrices) Let $\vec v$ be any real, three-dimensional unit vector and $\theta$ a real number. Prove that
注意到 迹, $tr(A\ket \psi \bra \psi)=\Braket{\psi|A|\psi}$,可以作为一个希尔伯特空间的自然内积。
commutator between two operators $A$ and $B$ is defined to be
if $[A,B]=0,AB=BA$ then we say A commutes with B.
anti-commutator is defined by
we say $A$ anti-commutes with $B$ if ${A,B}=0$
话说be defined to be 和 be defined by 有什么区别啊
Simultaneous diagonalization theorem
两个自伴算子可以协同对角化,当且仅当他们可以交换顺序。
先跳过,暂时不会(呜呜文威老师好像讲过我脑子笨啥都不记得了)
polar decomposition and SVD
unitary $U$ and positive operators $J$ and $K$ such that
$J\equiv \sqrt{A^\dagger A},K\equiv \sqrt{A A^\dagger}$ and if $A$ is invertible then $U$ is unique.
能SVD之后可以 施密特分解
The postulates of quantum mechanics
基本假设1、state space: Hilbert space
基本假设2、evolution: unitary transformation(封闭系统,连续时间)
$H$ is a fixed Hermitian operator known as the Hamiltonian of the closed system,从而可以谱分解,变成
传统称 $\ket E$ 为能量本征态 energy eigenstates 或者 stationary states,$E$ 是 $\ket E$ 的能量 energy。
最低的能量称为基态能量 ground state energy ,相应的能量本征态或者特征子空间称为基态。
之所以是稳定态,因为转变只可能是
2.56 Use the spectral decomposition to show that $K ≡ −i \log(U)$ is Hermitian for any unitary $U$, and thus $U = exp(iK)$ for some Hermitian $K$.
这个是说,任何一个 Hermitian 矩阵 和 一个 unitary 矩阵 对应。
值得注意的是,在一个开放的系统中,往往可以通过随着时间变化的哈密顿量 $H$ 的薛定谔方程来很好地近似。一般在量子系统的演变中,把演变都看作酉矩阵,但量子测量例外。
Quantum measurement
基本假设3、
state:
while
两个级联的测量是单个测量
两个非正交的状态不能被可靠地区分,与量子测量基本假设不符。
投影测量
观测是一个 Hermitian算符,$M=\sum_m mP_m$,$m$是特征值,$P_m$ 是投影。
那么会以 $p(m)=\Braket{\psi|P_m|\psi}$ 的概率 给出状态 $\frac{P_m\ket \psi}{ \sqrt{p(m)} }$
那么它的期望平均测量值为 $\mathrm{E}(M) = \Braket{\psi|M|\psi}$
定义 $\Braket M\equiv \Braket{\psi|M|\psi}$
它的标准差为 $[\Delta(M)]^2=\Braket{M^2}-\Braket{M}^2$
方差 $\Delta(M)=\sqrt{\Braket{M^2}-\Braket{M}^2}$,
如果系统处于本征态,那么测量的方差为0。
从而导出一些结论,如海森堡不确定性原理
这是本质的,尽管测量对系统有干扰,但那本不是测不准原理的解释。
例如,因为 $[X,Y]=2iZ$,从而对于量子态 $\ket 0$ 而言,有 $\Delta(X)\Delta(Y)\ge\Braket{0|Z|0}=1$
对于一个方向的观测
本征值也是 $-1/1$,相应的投影变换可以写作 $P+=\frac{1}{2}(I+\vec v\cdot \vec \sigma)$,$P-=\frac{1}{2}(I-\vec v\cdot \vec \sigma)$
我们可以定义 $E_m\equiv M_n^\dagger M_n$
量子测量:General measurements, projective measurements,POVMs
物理学家一般把量子测量看成是投影测量,也就是只会获得本征值的,其中一个原因是物理学的测量非常的粗暴,在量子计算中我们会用更精细的测量
通用测量在某些情况下在数学上更简化,举例来说,通用测量不需要满足 $PiP_j=\delta{ij}P_i$ 的条件
再比如,一些问题,如用光学方法分辨一些量子态,需要涉及通用测量而不是只有本征态的量子测量
只要酉变换(需要配合增大系统)配合上投影测量,就能实现通用观测。所以理论上来说投影测量也是足够了的。
一个 $\rm POVM$ 算子 $E_m$ 一定是 positive 的,特征值都是正的,positive 的也一定是自伴的。
基本假设4、用张量积来表示多个系统的复合
一些应用:
可以用一个量子比特传递两个经典比特的信息
The density operator
密度算子用来描述并不知道的某些量子系统的状态。
以 $p_i$ 的概率位量子态 $\ket {\psi _i}$,那么 ${p_i,\ket {\psi_i}}$ 称作 ensemble of pure states,同时定义密度算子
当然根据线性算子和矩阵的对应关系我们可以可以说密度矩阵 density matrix。
演化也是类似的,通过一个酉算子
对于一组测量 ${M_i}$ 测量得到状态 $m$ 的概率是
其中
而测量之后的状态推导为
有定理,$\rho$ 可以写作一系列的密度算子,当且仅当
Trace condition $\rho$ 迹为 $1$
Positivity condition $\rho$ 是 positive
上面的东西可以知道,用向量的方式和密度矩阵的方式来描述是等价的,一样的观测和演化,沿用量子力学基本假设。
如果$\rho = \ket \psi \bra \psi$ ,那么 $\rho$ 是 纯态 pure state,容易发现一个密度算子是纯态当且仅当它的平方的迹恰好为 1。
<—待整理—>
还有一种叫做混态的东西
两体纯态可以施密特分解,三体以上就不行了。
这里跳过一部分内容(指的是我把包括密度算符和贝尔不等式和各种东西都跳过了。学不会啊呜呜呜)
密度算子更容易描述收环境影响下的系统的情况
一个矩阵可以谱分解的充分必要条件是有 $n$ 个线性无关的特征向量。
另一个的作品的描述
外积 $\ket x\bra x$ 是一个算子,如果 $x$ 是空间中的向量
$M = \sum \ket {x_i} \bra {x_j}$ ,如果它的平方的 trace 为1,那么称为纯态
假设量子系统 $A$ ,不妨设他有一个纯态,系综
迹距离
也就是迹的距离
迹距离是一个距离
也就是两者做同一个测量,所能通过测量出现最大的距离
并且有:任何量子力学的操作下,迹距离只会减小。
测不准关系
本质上是,量子力学中对:密度矩阵要完正,POVM要完正,算子也要完正,这三者的完正德合并导致了测不准关系。
有一个混合态 $\rho_0,\rho_1$
$p_{suc} = p\Tr(M_0\rho_0)+(1-p)\Tr(M_1)\rho_1\le \frac{1-\Tr|p\rho-(1-p)\sigma|}{2}$
不可克隆原理
若可以复制,迹距离会变大,是不可能的
任何两个不正交的状态,不可能有一个物理过程把它克隆。
量子保真度
保真度是所有可能的最大的纯态的保真度来刻画。
量子保真度在量子力学允许的操作下只会越来越大,有一个凸性。
如果定义 $d(\rho,\sigma)=\sqrt{2(1-F(\rho,\sigma))}$ ,是一个距离。
量子Fisher信息
是一种均方差的推广,在纯态下就是一个均方差
就是纯态下的均方差的平均值
有不同的方法可以给出不确定度
比如熵,
电脑基础知识
图灵机模型
图灵机虽然是理论上的(无限纸带),但是在物理实现上是相当合理的。
程序:有限的有序的形如 $\Braket{q,x,q’,x’,s}$ 的集合,表示如果状态为 $q$,当前纸带的信息为 $x$,那么修改状态为 $q’$,修改纸带信息为 $x’$,指针头向 $s$ 移动。
Church-Turing thesis:……不再过多赘述(只是一个命题而不是一个定理)
丘奇图灵命题的伟大之处在于把当时一个模糊的称之为算法的东西给严格化证明了。如同实分析里面严格定义一个函数是“连续的”,既要严格,又要符合直观。
注意到每一台图灵机都可以被给出一个编号,
理论上来说,不管是两条纸带也好,到一个状态随机抛色子到下一个状态也好,都是可以被确定性图灵机模拟出来的(或者是遍历所有的可能性)。
Hilbert 的那个问题(用一个算法来证明所有东西)是 undecibability,有一些衍生的,像什么有一个算法来证明拓扑空间是不是同胚的也是 undecibale的。
通用图灵机:有点类似可编程的思想,把别的图灵机的状态写在纸带上。
3.5 图灵停机问题
程序 $Q(P,I)$ 在 $P(I)$ 停机的时候给出 $1$,否则给出 $0$。
程序 $U(P)$ 在 $Q(P,P) = 1$ 的时候不停机,否则停机。
若 $Q(U,U)=0$ 的时候,说明 $U(U)$ 不停机,但是 $U(U)$ 实际上是停机,引出矛盾
类似的 $Q(U,U)=1$ 的时候。
(好难
线路模型
可计算问题
$f(n) = O(g(n))$ 表示 $f(n)$ 的渐进上界不超过 $g(n)$
$f(n)=\Omega(g(n))$ 表示 $f(n)$ 的渐进下界不超过 $g(n)$
$f(n) = \Theta(g(n))$ 如果 $f(n)=O(g(n))=\Omega(g(n))$
数学分析里 $f(n)=o(g(n))$ 如果 $\lim \frac{f(n)}{g(n)}=0$
例如 $2n = O(2n^2),2^n=\Omega(n^3)$
强 丘奇图灵命题: 任何一个可计算的模型都可以被概率图灵机多项式模拟。
it is widely believed to be wrong
$\rm P,NP,coNP$ 众所周知了,都是判定性问题。
AI引论已经寄了呀——终期报告咋写啊www
$\rm P$ 就是说在最快的图灵机能够在多项式内判定的问题。
量子计算机不是图灵机,一般广泛认为给出 $m,l$ 问 $m$ 是否存在小于 $l$ 的非平凡因子就不是一个 $$ 问题
$\rm NP$ 就是,如果存在一个图灵机,以及给定的string $w$ ,在多项式的时间复杂度内,如果判定为 $Yes$,那么能够在 $q_Y$ 状态停机,如果判定为 $No$ ,那么可以试图进行判定发现失败然后在 $q_N$ 状态停机。
$\rm coNP$ 就是,能够对 $\rm NP$ 的反问题进行判定。
3.18 如果 $\rm coNP\not =NP$,则 $\rm NP\not= P$
$\rm P$ 的问题一定是 $\rm coNP$的,$\rm P$ 是 $\rm coNP$ 的子集。
两个问题差不多难,它们可以多项式规约。
$\rm NPI$ 在 $\rm NP$ 不在 $\rm P$ 中的,目前找不到,但是有些东西看上去很像是,比如判定两张图是不是同构的,比如质因数分解。
$\rm PSPACE$ 在图灵机中用多项式的空间,而不限制时间能解决的问题。
$\rm EXP$ : $O(2^{n^k})$
$\rm L$ : $O(log(n))$
$\rm L\subseteq P \subseteq NP\subseteq PSAPCE \subseteq EXP$ 看上去每个都不是等于,但都没有证明
$\rm BPP$ : 概率图灵机以 $3/4$ 的概率说明解是正确的或是解是错误的,在量子计算机上是$\rm BQP$
如果概率是 $1/2+\epsilon$,有:
计算能量
信物讲过的好像大概也许,当时觉得好厉害好厉害好厉害
但是都忘记了,想起来什么,信物最后一节课老师说,过了不需要多久,我们就会把知识给忘记,但是至少让我们知道当我们想要再去回顾一个东西的时候,我们应该怎么去回顾,应该到哪里去回顾。
可逆计算不需要消耗能量,然而信息的擦除是需要的,
Landauer’s principle 擦除一个信息至少需要 $k_BT\ln 2$ 的能量,$k_B$ 是玻尔兹曼常量
或者说,熵增加了 $k_B \ln 2$
那么怎么搞一台可逆计算呢,有一种好玩的模型 台球计算机 billiard ball computer
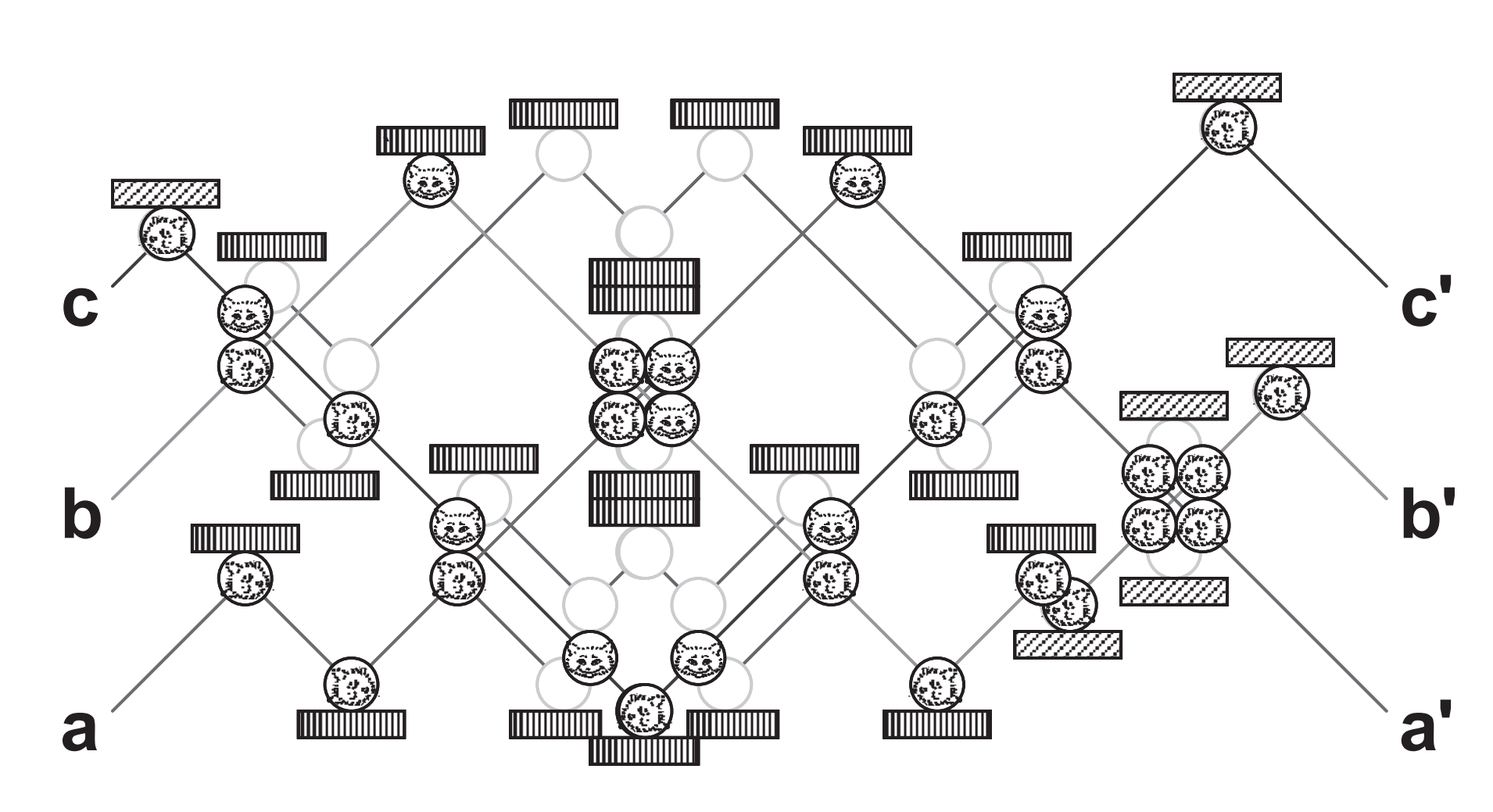
不得不说太优雅了(虽然扰动太大)。它实现了一个 Fredkin gates,控制比特(c)在1的时候swap另外两个比特的一个逻辑门。
Fredkin gates 是一种通用的逻辑门,可以模拟 and,not,crossover,fanout 之类的逻辑门。
Toffoli gates :$a,b,c\to a,b,c \oplus \lnot ab$
麦克斯韦妖的观测能量必须存储在其记忆中,不能违背朗达尔原则需要消耗能量,擦除有需要能量,所以并不违背热力学第二定律。
DNA计算机 and more
!好厉害!
用DNA计算机解决从 $j_1$ 到 $j_N$ 哈密顿路径问题的五个步骤
1、随机生成一条路径。
把节点和边的DNA混合起来,PCR
$x_ix_j$ 表示一条路, $x_ix_i$ 表示顶点到顶点。
2、只保留从 $j_1$ 到 $j_N$ 的路径
扩增以 $x{j_1}$ 开头的和 $x{j_n}$ 结束的双链,
3、只选择长度为 $N$ 的路径
根据长度来分离,电泳
4、只选择经过每个节点恰好一次的路径
把DNA分解成单链,对于每个顶点,把可能的顶点链筛掉。退火。
5、检验是否还有幸存下来的 DNA。
为了正确率高,需要许多的DNA($\ge 10^{14} $),碱基对($\approx 30 $)
模拟计算 是很高效的东西,比如 模拟电路,与数字电路相比,模拟电路能保存的信息在理想情况下几乎没有限制,但是容易受到噪声干扰。
量子计算机是模拟计算机吗?它能存储连续的参数。
但是能够证明噪声对量子计算机的干扰可以有效地被数字化,因此量子计算机可以保持其优势,在有限的噪声中。
分布式计算:众所周知。
以及一些数字游戏(相比于量子计算机这种容易在物理中实现的计算模型)
Minsky machines (图灵机等价):有 $k$ 个寄存器存储非负信息,两种节点,一种是使得寄存器 $r_j$ 增加一,并进行下一个命令,一种是使得寄存器 $r_j$ 减少一,并根据 $r_j$ 是否为 $0$,走 $A$ 线路或者 $B$ 线路。
Vector game ,Franctran……
量子线路
第一部分是,如何用简单的量子门模拟所有的量子门
对于可行性而言,我们需要这些:
1、任何一个多比特量子门都可以用单比特量子门和多比特控制门来实现。
2、任何一个多比特控制门,可以用单比特量子门和CNOT实现。
3、任何一个CNOT门都可以减小到
4、任何一个单比特量子门都可以被 H门,S门,T门搞定。
Single qubit operations
常用的单比特量子门:
Pauli-X门,$X\equiv \begin{pmatrix}0&1\1&0\end{pmatrix}$,效果:$\ket 0 \to \ket 1,\ket 1 \to \ket 0$
Pauli-Y门,$Y\equiv \begin{pmatrix}0&-i\i&0\end{pmatrix}$ 效果为绕布洛赫球 $Y$ 轴旋转角度 $\pi$
Pauli-Z门,$Y\equiv \begin{pmatrix}1&0\0&-1\end{pmatrix}$ 效果为绕布洛赫球 $Z$ 轴旋转角度 $\pi$
Hadamard(H)门 $H\equiv \frac{1}{\sqrt{2}}\left( \begin{array}{} 1 & 1 \1 & -1 \end{array} \right)$
Phase(S)门 $S\equiv \begin{pmatrix}1&0\0&i\end{pmatrix}$
$\pi$/8(T)门 $T\equiv \begin{pmatrix}1&0\0&\exp(i\pi/4)\end{pmatrix}$, $T$ 是对角线为 $\begin{pmatrix}exp(-i\pi/4)&0\0&\exp(i\pi/4)\end{pmatrix}$ 的矩阵的归一化
$RX(\theta) = e^{-i\theta X/2} = \cos(\theta/2)I - i\sin(\theta/2)X =\left( \begin{array}{} \cos(\theta/2) & -i\sin(\theta/2) \-i\sin(\theta/2) & \cos(\theta/2) \end{array} \right)$
$RY(\theta) = e^{-i\theta Y/2} = \cos(\theta/2)I - i\sin(\theta/2)Y =\left( \begin{array}{} \cos(\theta/2) & -\sin(\theta/2) \\sin(\theta/2) & \cos(\theta/2) \end{array} \right)$
$RZ(\theta) = e^{-i\theta Z/2} = \cos(\theta/2)I - is\in(\theta/2)Z =\left( \begin{array}{} e^{-i\theta/2} & 0 \0 & e^{i\theta/2} \end{array} \right)$
由于全局相位不发挥作用,$RZ$ 等价于 $\left( \begin{array}{} 1 & 0 \0 & e^{i\theta} \end{array} \right)$
4.2
也可以用泰勒展开
4.3 $T = R_z(\pi /4)$
Theorem 4.1:Z-Y decomposition for a single qubit:任何一个酉矩阵 $U$ 都存在实数 $\alpha ,\beta ,\gamma,\delta$ 写成
这一段好难啊,我觉得我不太能理解关于$exp(i\theta)$ 相关的东西,既然全局相位是无关的为什么还要加上 $e^{i\alpha}$
上面那个定理是为了证明下面的推论,据说是构建受控多量子比特单一操作的关键。
Corollary 4.2: 对于任何酉门 $U$ ,存在酉算子$A,B,C$ ,满足 $ABC=I$ ,$U=e^{ia}AXBXC$ ,
4.13 $HXH=Z,HYH=-Y,HZH=X$
Controlled operations
可能看上去我需要学一下 Tex ,那种可以画出来量子门电路的。诶,之后再说。
如何对任意一个 U 实现控制门?如果我们有的只是 CNOT门,可以构造出来,方法如下。
首先,$U=e^{ia}AXBXC$ ,其中 $ABC=1$
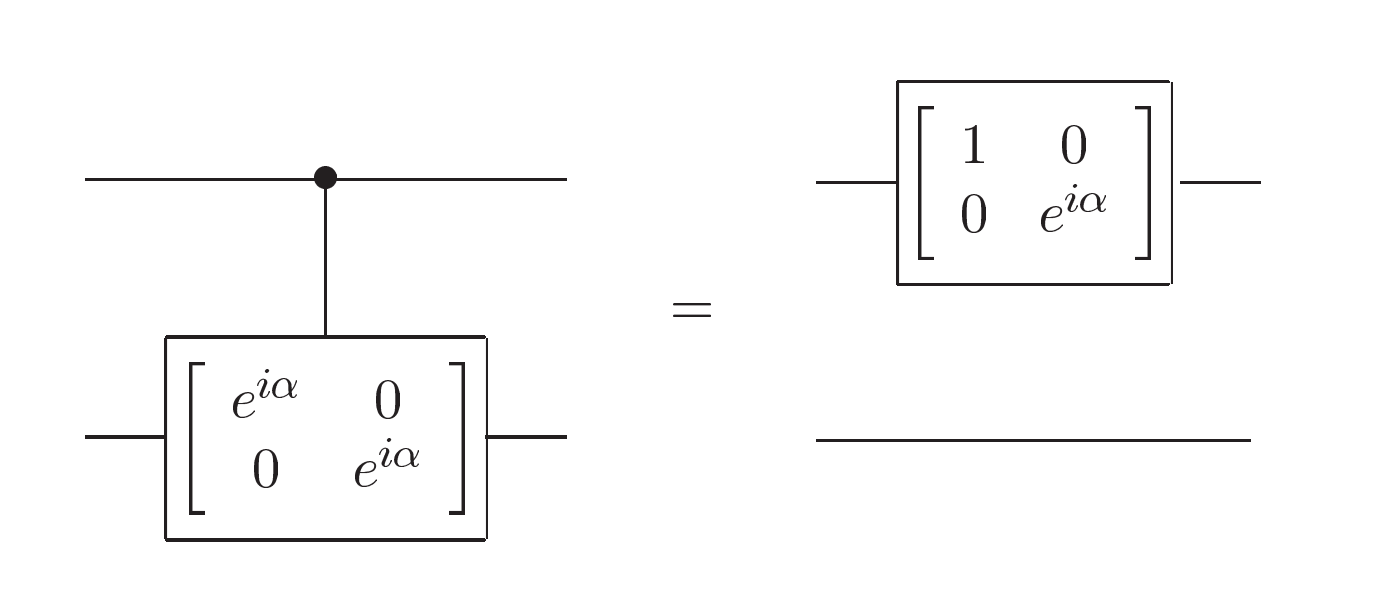
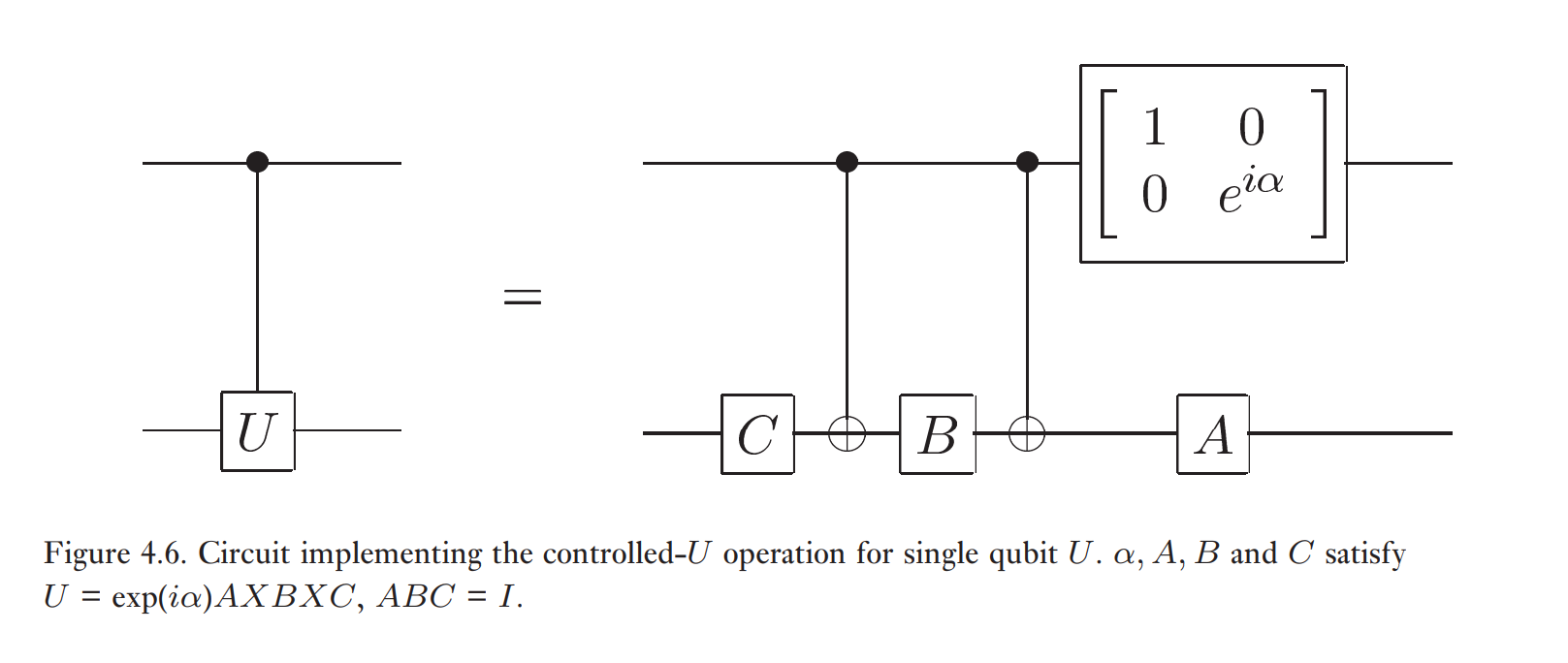
方法可以扩展到用 $n$ 个比特全为 $1$ 的时候对 $k$ 个比特使用酉门。
例如:若 $V^2=U$
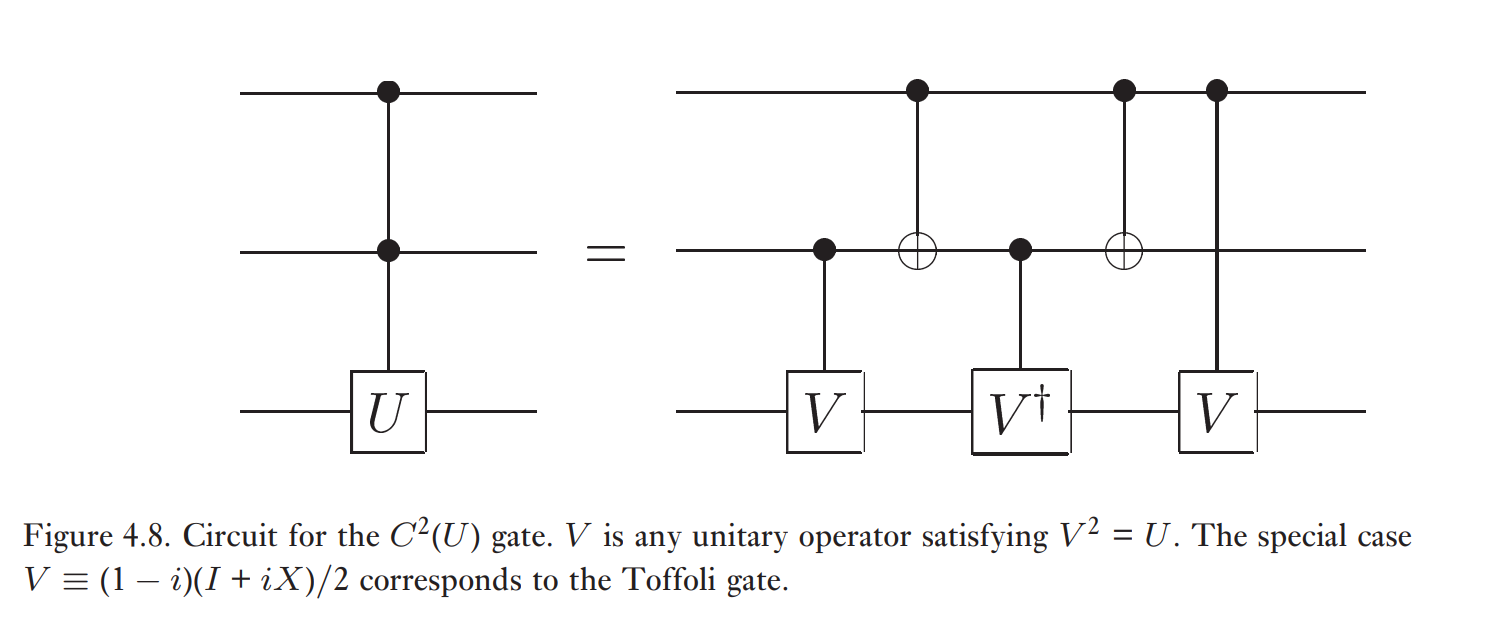
当 $V=(1-i)(I+iX)/2$ 的时候就得到了 Toffoli 门。
引入辅助比特,可以做下面的事情
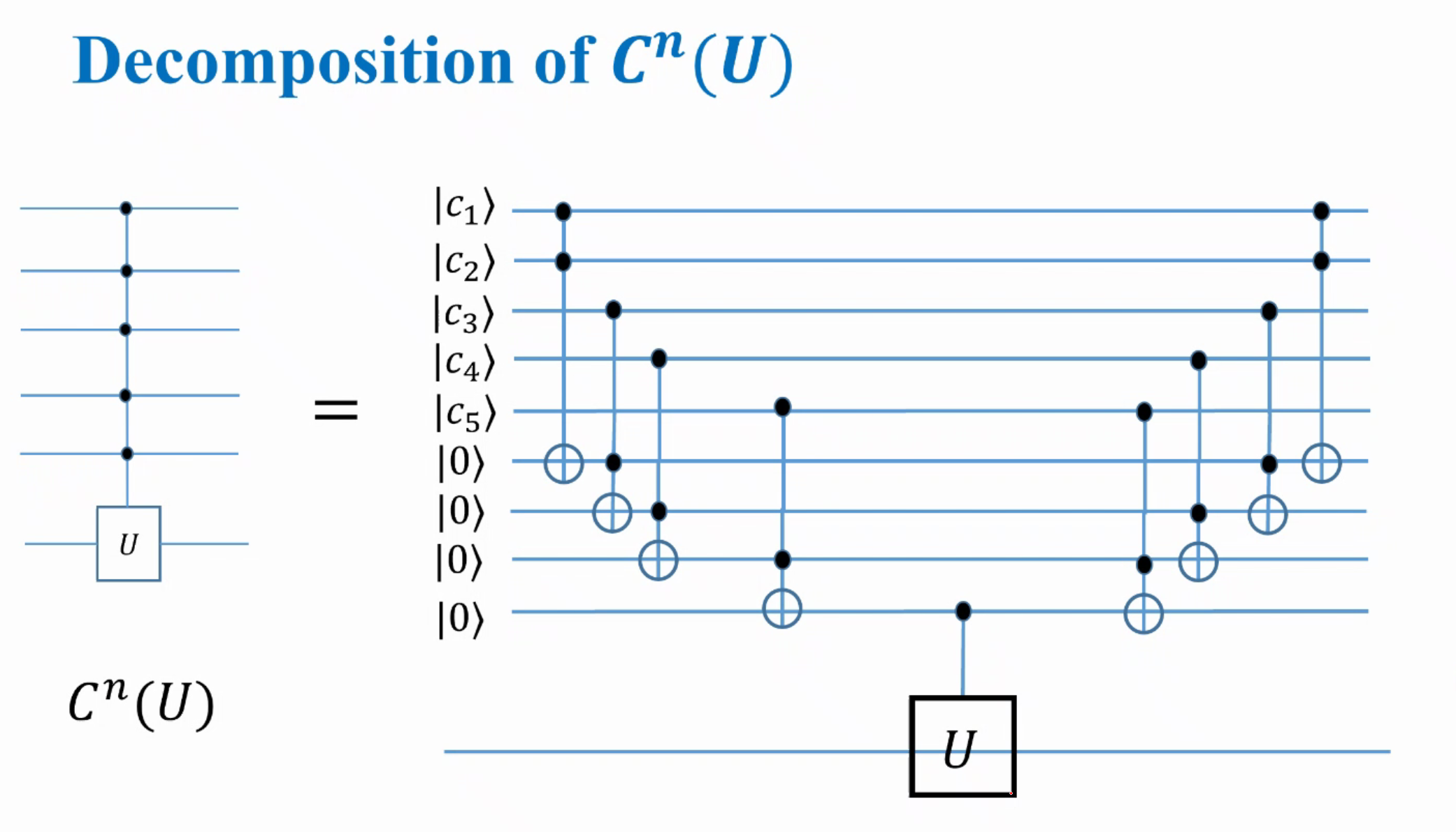
Two level unitary gates are universal
TLU指的是除了某两行和某两列是有值,剩下的除了对角是1,剩下都是0.
任何一个$dd$的矩阵,都可以存在 $\le d (d-1)/2$ 个这样的TLU,变成这些东西的乘积。
具体的分解方法为:高斯消去法。
Approximateing unitary operators
定义两个酉算子的距离,所有量子态的最大
$\norm{U-V}:=\max _\ket \psi \norm {U-V}\ket \psi$
现实中很难做到,现实中上人们可能更考虑对于所有量子态的期望值最小
给定 $\ket \psi$ 和一系列的 $\rm POVM$ $M_i$,作用在 $U\ket \psi$ 和 $V \ket \psi$ 上
对于两个测量后的结果 $p_i,q_i$,有 $|p_i-q_i|\le 2 \norm {U-V}$
$\ket \Delta:=(U-V)\ket \psi$
有 $\norm {UtU{t-1}…U1-V_tV{t-1}…V_1}\le\sum_i\norm{U_i-V_i}$
Gray code:每次变换一个比特一步一步把 $s$ 变换成 $t$。
任何unitary都可以分解成 Single Qubit unitary 和 CNOT
那么怎么实现Single Qubit呢?
事实上,Single Qubit可以只用 Hadamard+phase+T
T:rotation by $\pi/4$ around $z$ axis
HTH: rotation by $\pi/4$ around $x$ axis
THTH = rotation by $\theta$ around $\hat n$ axis
$\hat n=(\cos \pi/8,\sin \pi/8,\sin \pi/8),\theta=2\arccos (\cos^2\pi/8)$
而这个 $\theta$ 是一个无理数,在圆上旋转多次可以转出所有角度。
转动 N 次,用鸽巢原理,精度可以调得足够小。
现在,我们可以在 $\hat n$ 这个神奇的方向旋转任意的角度。
如果我们再做一次 $H$ ,就能在另一个神奇的方向 $\hat m=(\cos \pi/8,-\sin \pi/8,\cos \pi/8)$ 做任意角度的旋转。
好了,出来了!虽然有一点精度问题,简单的达到 $\epsilon$ 的精度的话,需要 $1/\epsilon$ 个门。
后来又有一种挺好的方法可以用 $log$ 的方法了
Solovay-Kitaev Theorem
不动了,这个模拟需要的门据说大概在 $\log 1/\epsilon$ 。
$[U,V]=UVU^{-1}V^{-1}$
定义 $S_\epsilon=\set{U\in SU(2)\mid \norm{I-U}\le\epsilon}$ ,为以 $I$ 球心的,距离在 $\epsilon$ 内的,
听说要用到李群的东西,呜呜呜
如果我们能找到一组Gate,使得在这个球里面足够的密……
量子算法!
Deutch-Jozsa算法里面,既然要设计Bf的量子线路,可以理解为已经知道了f的数学表达式了吗,如果知道了表达式直接进行表达式的分析,就不需要遍历查询了,那么经典的复杂度就没有指数次了。如果不知道数学表达式,又怎么设计Bf对应的量子线路呢?还有Grover算法里的无结构,无结构那么Of又是怎么设计的呢?
算法概要
量子算法 ,量子程序理论,量子编译,微结构与脉冲控制,量子硬件
有很多复杂度方面的比较,查询复杂度(关注调用某一子过程的次数)
有思想性的量子算法不多,Shor算法算一个,Grover算法算一个,HHL算法可能也算一个,但是有了这样的有思想的算法的出现可以出现很多不同的算法。
往上一个层次是基础性的量子算法,比如说图论相关的,量子游走搜索问题,量子振幅放大等。有很多计算机理论背景的人在做。
再往上一个层次有一些应用性的量子算法。x幼具体的严谨的算法的分析。
关注量子算法的驱动力是,计算复杂性的角度量子计算有优势,
时间线:
1、初始阶段,为量子而问题,(但很有思想!)
1985 Deutsch 算法(在一篇量子图灵机的论文中)
1992 Deutsch-Jozsa 算法
1993 BV 算法
1994 Simon 算法
2、质变阶段,为问题而量子
1994 Shor算法
1996 Grover算法
1993 量子游走
3、面向大数据环境的量子算法,基础还是需要一些
2009 HHL 算法(解线性方程组的,但没法和Shor算法,Grover算法媲美)
量子机器学习算法
4、这几年流行的,(面向NISQ时代的量子算法?),基于变分量子电路的量子-经典混合算法
2014 QAOA
2014 VQE
基础QwQ
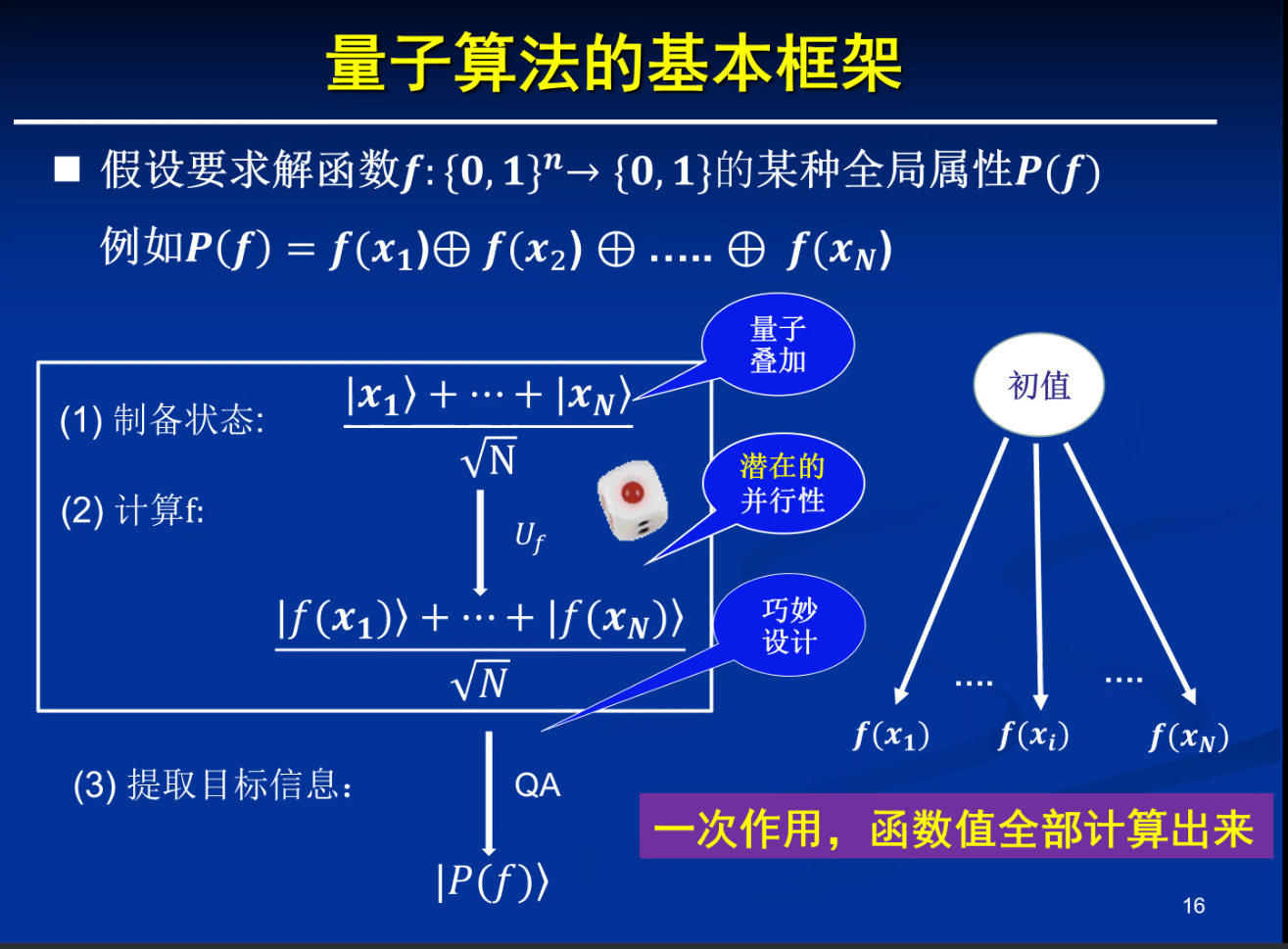
Dtutsch-Jozsa算法 概要
给定一个布尔函数,判断函数是平衡函数(一半为零,一半为一)还是常量函数(全部相同)
原来是 $\ket {f(x_i)}$,但是这个算法能把它变到相位里面 $(-1)^{f(x_i)}\ket x_i$,在相位上就可以进行干涉。
然后再做 $H^{\otimes n}$ 得到一个 $\ket \phi$ 。
Grover算法 概要
用于解决无序数据库搜索问题,该问题可以一般化为振幅(概率)放大。
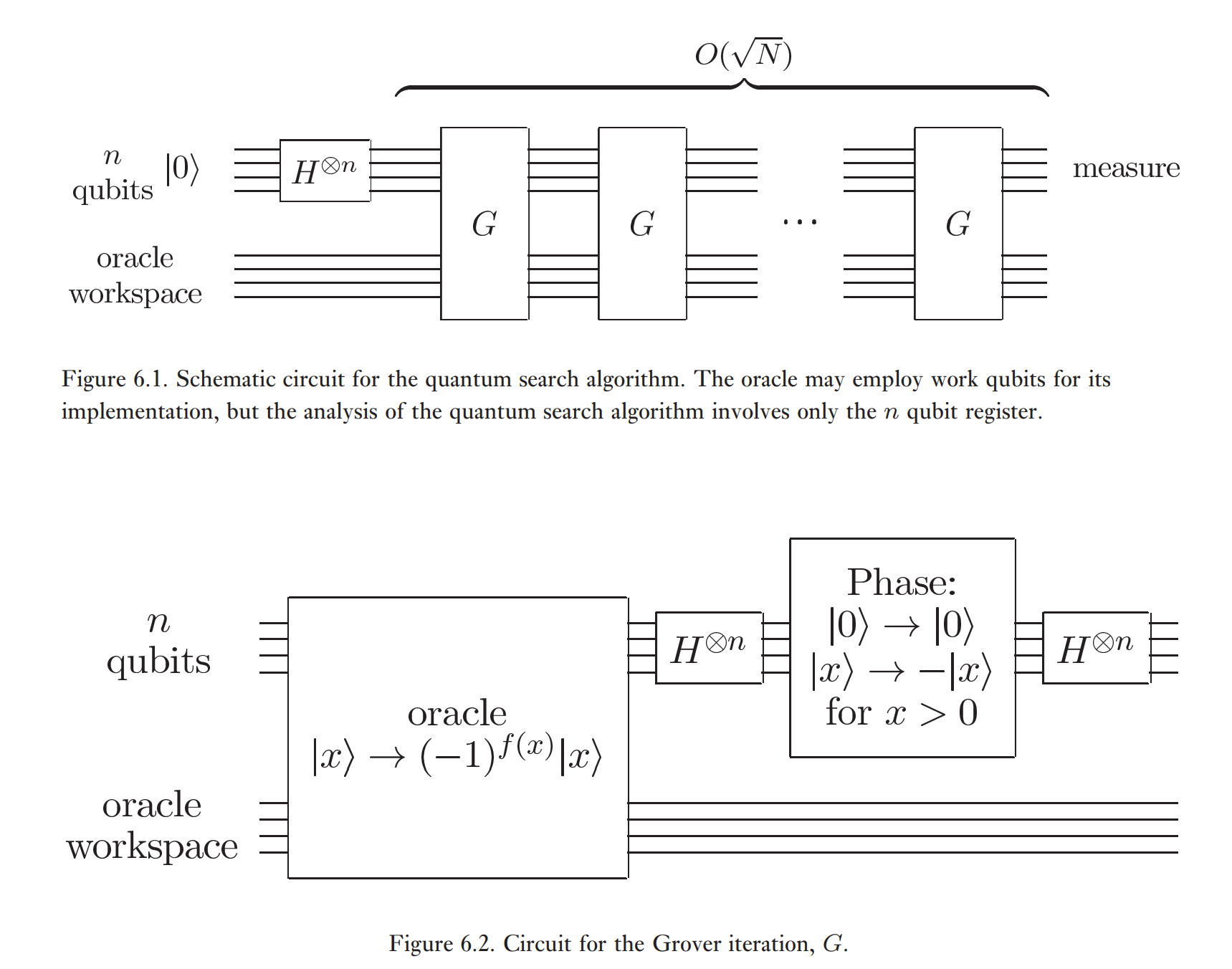
$G=H^{\otimes n} (2\ket 0 \bra 0 - I) H^{\otimes n} O_f$ ,$O_f \ket x = (-1)^{f(x)} \ket x$
不严格的,几何直观:
设要求的集合的叠加态为 $A$,不要的集合的叠加态为 $B$,显然 $A$ 和 $B$ 正交且张成整个空间。
$\phi = \sqrt{\frac{M}{N}}\ket A + \sqrt\frac{N-M}{N}\ket B$ ,在线性空间中,$\ket \phi$ 和 $\ket B$ 有夹角 $\theta =\arcsin \sqrt\frac{M}{N}\approx \sqrt\frac{M}{N}$。
不严格的分析,若 M 远小于 N。

更多讨论
M为止怎么办??
1、用量子计数估算目标点的数目再搜索。
2、指数式猜测逐步扩大搜索次数。
对该算法做一些改造,能够在 $M$ 已知的时候让成功概率做到 $100\%$ ,且平方加速
在目标占比未知的情况下,百分之百成功和平方加速不可兼得。(有证明)
成功概率为 $\sin(2k+1)\theta$ ,是振荡的,不够鲁棒,如何克服?
Grover 后来提出了一个成功概率单调递增的方法,但失去了平方加速。
从 Grover 算法到基于量子游走的搜索算法
是一种特殊图(完全图)上的游走搜索算法
从 Grover 算法到量子振幅放大
设算法 $A\ket 0 = \sqrt p \ket G + \sqrt{1-p} \ket B$
可以构造量子计算过程 $Q$ 使得
$Q^m A \ket 0 = \alpha \ket G + \beta \ket B$,$m$ 在 $\sqrt {1/p}$ 级别
其中 $|\alpha|^2 \to 1,Q=A(2\ket 0\bra 0 - I)A^{-1}S_x$
Shor算法 概要
精髓啊,灵魂啊

本质上是寻找函数的周期
解决一个求阶问题:给定 $x<n$ ,求大于 $0$ 的最小整数 $r$ 使得 $x^r\equiv 1\mod n$
或许应该看看Shor的
1、从因式分解到求阶问题的归约,成功概率 $\ge \frac{1}{2}$
2、求阶算法测 Reg1 得到 $\ket c$ 满足 $|\frac{c}{q}-\frac{d}{r}| \le \frac{1}{2q}$ 的概率 $\ge \frac{4}{\pi^2}$
3、两次求阶、连分法后,计算 $lcm(r_1,r_2)=r$ 的概率 $\ge \frac{1}{4}$
因此总的成功概率 $\ge \frac{1}{2} (\frac{4}{\pi^2})^2\frac{1}{4}$ 为常数。
$U_f$ 复杂度为 $O(\log^3n)$ ,QFT的复杂度为 $O(\log^2n)$ ,连分法的复杂度为 $O(\log ^3 n)$。
本质上是寻找函数的周期
连分法:
如何根据 $|\frac{c}{q}-\frac{d}{r}| \le \frac{1}{2q}$ ,在知道 $\frac{c}{q}$ 的时候得到 $r$ 。(已知 $c,q$,且 $d\in\set{0,1,\dots ,r-1}$,$r$ 为止。
Fact1:至多存在一个 $\frac{d}{r}$ 满足 式子,且 $0<r<n$。
Fact2:存在既约分数 $\frac{d}{r}$ 满足 式子,则该分数可通过对 $\frac{c}{q}$ 进行连分数展开得到。
类似辗转相除,对有理数可以有限逼近,实数可以无穷逼近
QFT的电路实现
咕
量子相位估计
给定一个酉矩阵 U 及它的一个特征向量 $\ket u$ ,假设其对应的特征值为 $e^{2\pi i\theta}$,即 $U\ket u=e^{2\pi i\theta}\ket u$,其中 $\theta\in[0,1)$ 相位估计问题就是要估计出 $\theta$ 的值。
实现方法与 Shor 算法类似,需要一个逆傅里叶变换。
需要受控 $U_j$ 门。
解隐含子群问题
给定一个群 $G$ ,将群映射到一个有限的集合 $G\to X$,假定存在一个子群 $H$ ,且任何 $g_1,g_2 \in G$,$f(g_1)=f(g_2)\iff g_1H=g_2H$。
Problem:找到这个 $H$
目前结果:阿贝尔群有多项式查询复杂度的,多项式次调用 $f$ 。
量子查询模型
Shor,Grover,Deutsch-Jozsa 共性
给定来自函数类 $C$ 中的某个 $f$ ,希望尽快可能少地访问 $f$ 而求解出 $f$ 的某种特性 $P_f$
这个 $f$ 是黑盒还是白盒?
量子查询模型更抽象的形式
给定布尔函数 $f:{0,1}^n\to{0,1}$,对任意输入 $x$,希望通过尽可能少地访问 $x$ 的比特位而得到函数值 $f(x)$。
比如 $f(x)$ 是判断 $x$ 的奇偶性,那么只要求 $x$ 的最后一位就行了。
DJ问题等价于计算函数 $f_1(x)=0(|x|=n/2),1(|x|=0,n)$
解方程算法
这两个算法的解藏在振幅里面,并不如前面一些算法来得优美。
HHL算法
解线性方程组的 $Ax=b$
哈密顿量模拟的视角
思想就是快速生成一个向量逼近
$A=\sum_i\lambda_i\ket {u_i}\bra {u_i}$
$x=A^{-1}b =\sum_{i}\frac{b_i}{\lambda_i} \ket {u_i}$
CKS算法
首先有近似分解 $A^{-1}=\sum_ja_je^{-iAt_j}$
存在量子过程有效模拟 $e^{-iAt_j}$
进而模拟线性组合 $\sum_j a_j e^{-iAt_j}$ 从而实现 $A^{-1}$
量子傅里叶变换
考虑把 $k$ 用二进制展开
